카운팅 정렬
시간 복잡도는 O(n+k) (k는 데이터의 최댓값을 의미한다.)
카운팅 정렬은 가장 큰 데이터에 따라 효율이 좌지우지된다.
쉽게 설명하자면 특정 데이터의 개수(1이 두 개 있다면 2)를 데이터의 값에 대응하는 위치에 저장한 뒤, 자신의 위치에서 앞에 있던 값을 모두 더한 배열을 만든 뒤, 거기서 데이터가 들어가야 할 위치를 찾아내는 정렬 알고리즘이다.
이 경우에 데이터의 최댓값을 k라 두면, 시간 복잡도는 O(n+k).
하지만, 만약 k가 억 단위를 넘어간다면?
n이 아무리 작아도 동작시간이 크다.
반대로 k가 매우 작다면, 오히려 선형시간의 효과를 볼 수 있다.
즉, k가 작다는 조건이라면 매우 효율적인 정렬.
또한 카운팅 정렬은 배열을 사용하는 특성상, 정수라는 전제를 깔고 한다.
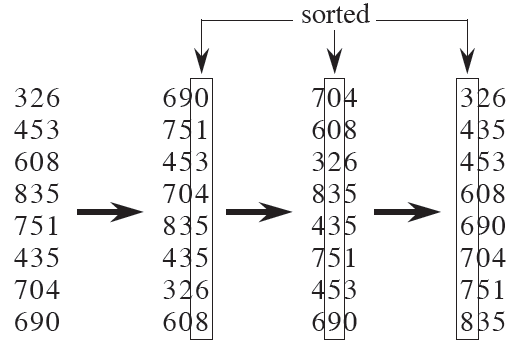
카운팅 정렬 예제
http://www.cs.miami.edu/home/burt/learning/Csc517.091/workbook/countingsort.html
Counting Sort
This is an animation of the counting sort algorithm found in CLR's Algorithms book. Array C (counting array): PSEUDOCODE FOR COUNTING SORT (taken from CLR) Initialize counting array to all zeros. Count the number of times each value occurs in the input. Mo
www.cs.miami.edu

카운팅 정렬 파이썬 코드
def counting_sort(A, k) :
B = [-1] * len(A)
C = [0] * (k+1)
for a in A :
C[a] += 1
for i in range(k):
C[i+1] += C[i]
for j in reversed(range(len(A))):
B[C[A[j]]-1] = A[j]
C[A[j]] -= 1
print(B)
return B
ZDD = [2, 0, 2, 0, 213, 3214, 4312,12, 2314, 2345123, 13412342]
k = 13412342
print(counting_sort(ZDD, k))과정 + 결과. -1은 null 값이라 봐도 무관.

카운팅 정렬 C 코드
#include <cstdio>
#define MAX_SIZE 1000
#define MAX_NUM 10000
int main(){
int N, A[MAX_SIZE+1], B[MAX_SIZE+1], count[MAX_NUM+1], countSum[MAX_NUM+1];
//수열의 길이 N은 MAX_SIZE이하여야합니다.
scanf("%d", &N);
//count배열을 모두 0으로 초기화
for(int i = 0; i<= N ; i++)
count[i] = 0;
//수열 A에 입력되는 수는 MAX_NUM 이하여야합니다.
for(int i =1 ; i<= N ; i++){
scanf("%d", &A[i]);
//숫자 등장 횟수 세기
count[A[i]]++;
}
//누적합 구성
countSum[0] = count[0];
for(int i = 1 ; i<= MAX_NUM ; i++)
countSum[i] = countSum[i-1]+count[i];
//뒤에서 부터 수열 A 순회한다.
for(int i = N ; i >= 1; i--){
B[countSum[A[i]]] = A[i];
countSum[A[i]]--;
}
//수열 A를 정렬한 결과인 수열 B를 출력한다.
for(int i =1 ; i<= N ; i++)
printf("%d ", B[i]);
}출처: https://tinyurl.com/y287lhew
TISTORY
나를 표현하는 블로그를 만들어보세요.
www.tistory.com
'알고리즘 공부' 카테고리의 다른 글
| 15. 그리디 알고리즘 (동전, 거스름돈 문제) (0) | 2019.10.03 |
|---|---|
| 14. 다익스트라 알고리즘 (0) | 2019.10.03 |
| 12. 기수 정렬 (A.K.A Radix sort) (0) | 2019.09.29 |
| 11. 쉘 정렬 (0) | 2019.09.29 |
| 10. 병합 정렬(A.K.A merge sort) (0) | 2019.09.28 |



