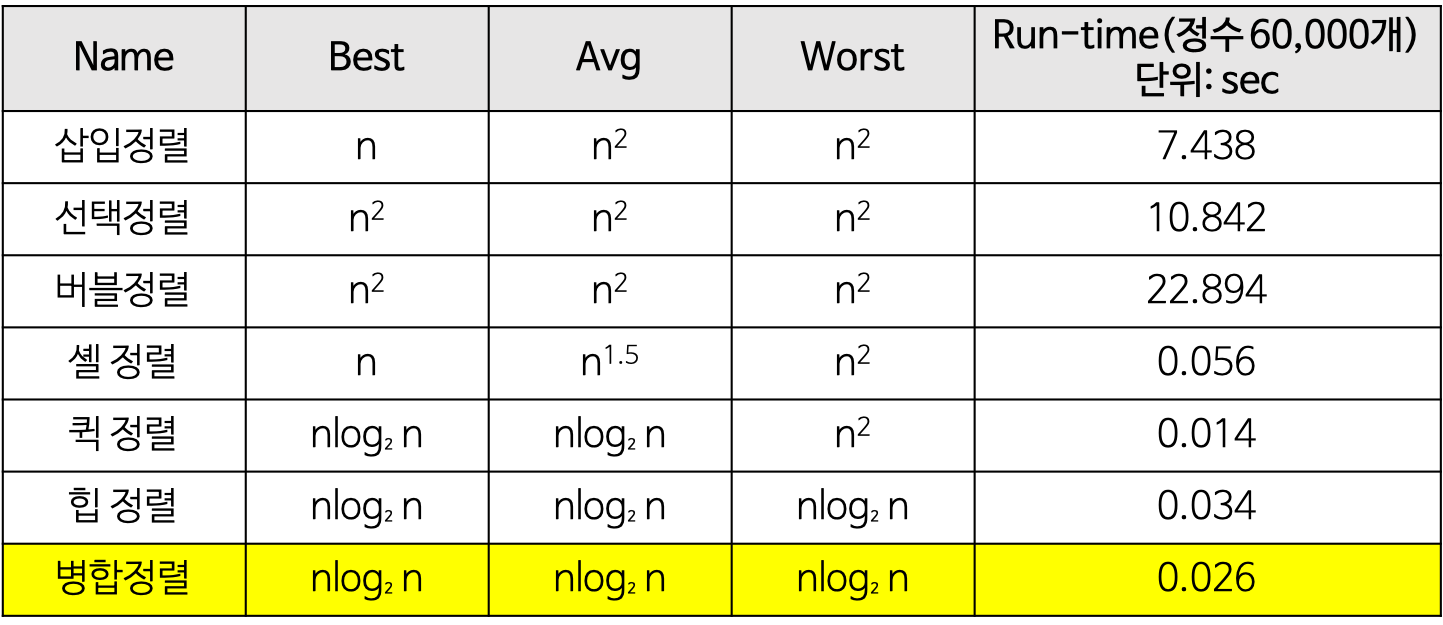
병합 정렬
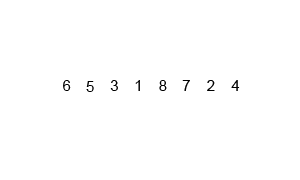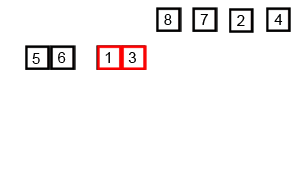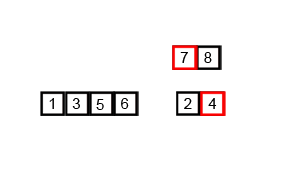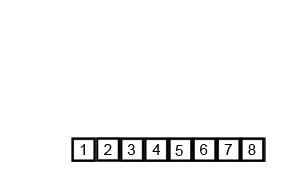
개발자는 존 폰 노이만, 원소 개수가 1 또는 0이 될 때까지 두 부분으로 쪼개고 쪼개서 자른 순서의 역순으로 크기를 비교해 병합해 나간다.
병합된 부분 안은 이미 정렬되어 있으므로 전부 비교하지 않아도 제자리를 찾을 수 있다.
대표적인 분할 정복 알고리즘으로 존 폰 노이만의 천재성을 엿볼 수 있는 알고리즘이다.
성능은 아래의 퀵 정렬보다 전반적으로 뒤떨어지고, 데이터 크기만한 메모리가 더 필요하지만 최대의 장점은 데이터의 상태에 별 영향을 받지 않는다는 점'이다.
힙이나 퀵의 경우에는 배열 A[25]=100, A[33]=100인 정수형 배열을 정렬한다고 할 때, 33번째에 있던 100이 25번째에 있던 100보다 앞으로 오는 경우가 생길 수 있다.
그에 반해서 병합정렬은 정렬되어 있는 두 배열을 합집합 할 때 이 알고리즘의 마지막 단계 만을 이용하면
가장 빠르게 정렬된 상태로 합칠 수 있다.
https://youtu.be/XaqR3G_NVoo
병합 정렬은 다음의 단계들로 이루어진다.
- 분할(Divide): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
- 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용.
- 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.
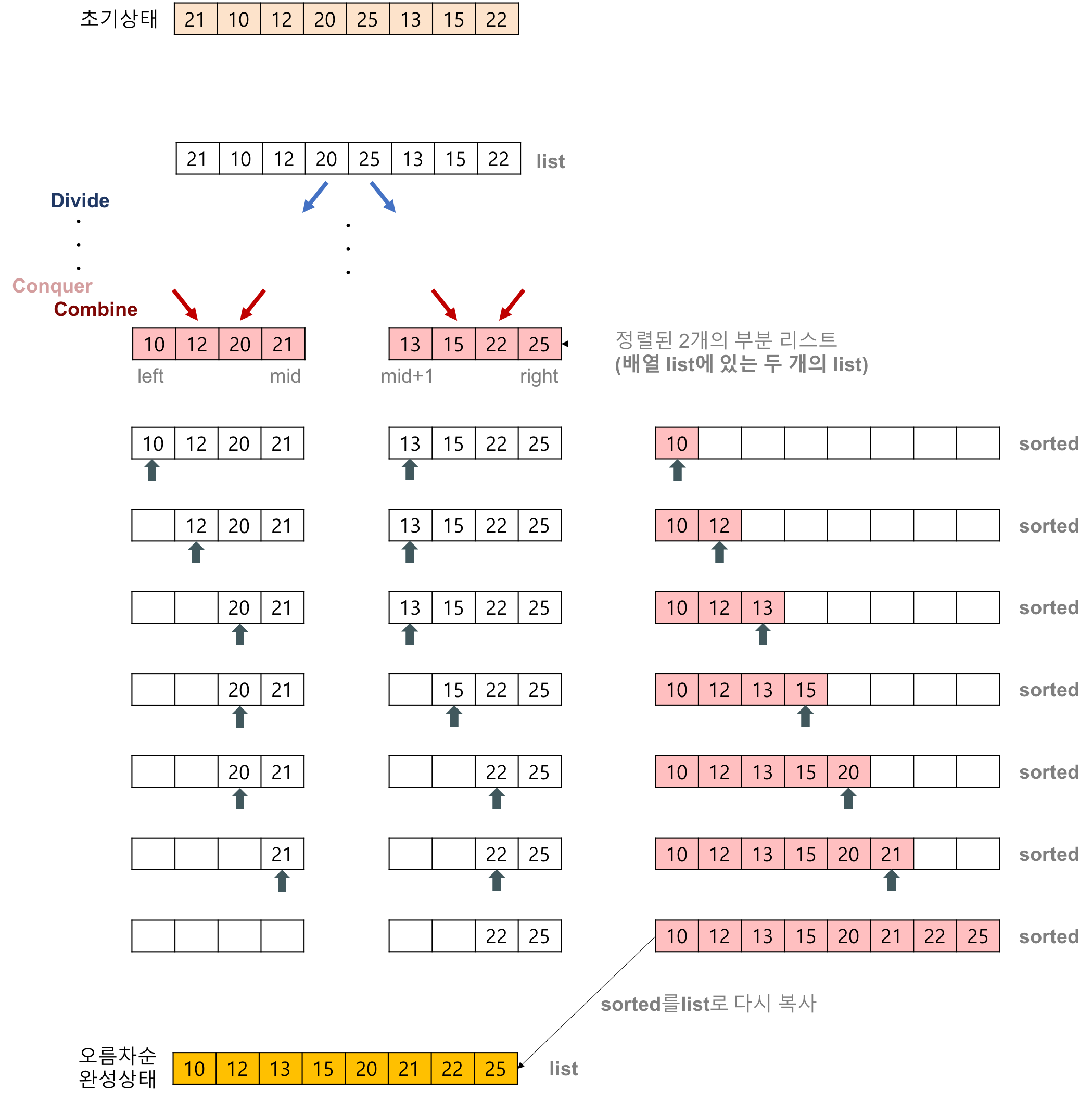
병합 정렬 예제
배열에 27, 10, 12, 20, 25, 13, 15, 22이 저장되어 있다고 가정하고 자료를 오름차순으로 정렬해 보자.
2개의 정렬된 리스트를 합병(merge)하는 과정
1. 2개의 리스트의 값들을 처음부터 하나씩 비교하여 두 개의 리스트의 값 중에서 더 작은 값을 새로운 리스트(sorted)로 옮긴다.
2. 둘 중에서 하나가 끝날 때까지 이 과정을 되풀이한다.
3. 만약 둘 중에서 하나의 리스트가 먼저 끝나게 되면 나머지 리스트의 값들을 전부 새로운 리스트(sorted)로 복사한다.
4. 새로운 리스트(sorted)를 원래의 리스트(list)로 옮긴다
병합 정렬 C 예제.
# include <stdio.h>
# define MAX_SIZE 8
int sorted[MAX_SIZE] // 추가적인 공간이 필요
// i: 정렬된 왼쪽 리스트에 대한 인덱스
// j: 정렬된 오른쪽 리스트에 대한 인덱스
// k: 정렬될 리스트에 대한 인덱스
/* 2개의 인접한 배열 list[left...mid]와 list[mid+1...right]의 합병 과정 */
/* (실제로 숫자들이 정렬되는 과정) */
void merge(int list[], int left, int mid, int right){
int i, j, k, l;
i = left;
j = mid+1;
k = left;
/* 분할 정렬된 list의 합병 */
while(i<=mid && j<=right){
if(list[i]<=list[j])
sorted[k++] = list[i++];
else
sorted[k++] = list[j++];
}
// 남아 있는 값들을 일괄 복사
if(i>mid){
for(l=j; l<=right; l++)
sorted[k++] = list[l];
}
// 남아 있는 값들을 일괄 복사
else{
for(l=i; l<=mid; l++)
sorted[k++] = list[l];
}
// 배열 sorted[](임시 배열)의 리스트를 배열 list[]로 재복사
for(l=left; l<=right; l++){
list[l] = sorted[l];
}
}
// 합병 정렬
void merge_sort(int list[], int left, int right){
int mid;
if(left<right){
mid = (left+right)/2 // 중간 위치를 계산하여 리스트를 균등 분할 -분할(Divide)
merge_sort(list, left, mid); // 앞쪽 부분 리스트 정렬 -정복(Conquer)
merge_sort(list, mid+1, right); // 뒤쪽 부분 리스트 정렬 -정복(Conquer)
merge(list, left, mid, right); // 정렬된 2개의 부분 배열을 합병하는 과정 -결합(Combine)
}
}
void main(){
int i;
int n = MAX_SIZE;
int list[n] = {21, 10, 12, 20, 25, 13, 15, 22};
// 합병 정렬 수행(left: 배열의 시작 = 0, right: 배열의 끝 = 7)
merge_sort(list, 0, n-1);
// 정렬 결과 출력
for(i=0; i<n; i++){
printf("%d\n", list[i]);
}
}
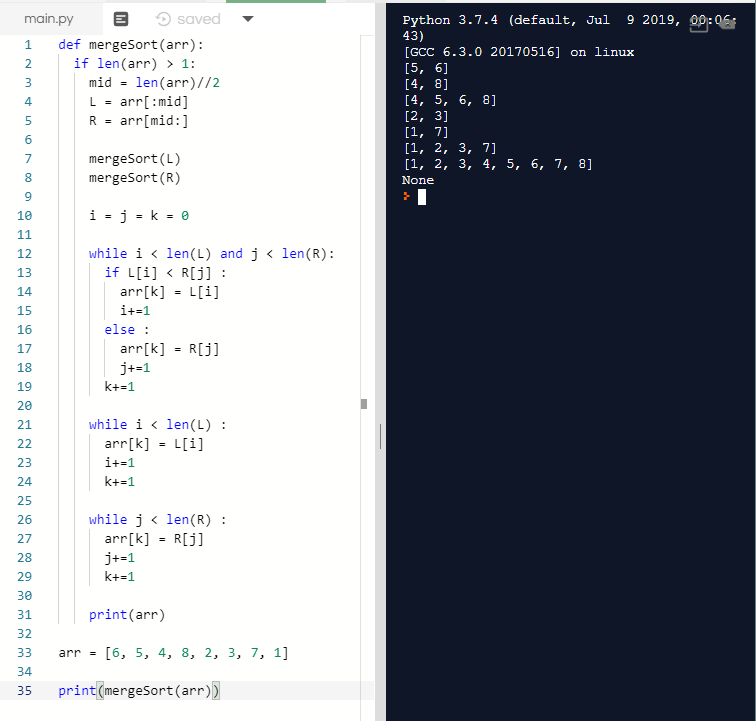
//https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html병합 정렬 파이썬 코드
def mergeSort(arr):
if len(arr) > 1:
mid = len(arr)//2
L = arr[:mid]
R = arr[mid:]
mergeSort(L)
mergeSort(R)
i = j = k = 0
while i < len(L) and j < len(R):
if L[i] < R[j] :
arr[k] = L[i]
i+=1
else :
arr[k] = R[j]
j+=1
k+=1
while i < len(L) :
arr[k] = L[i]
i+=1
k+=1
while j < len(R) :
arr[k] = R[j]
j+=1
k+=1
print(arr)
arr = [6, 5, 4, 8, 2, 3, 7, 1]
print(mergeSort(arr))결과.
병합정렬 (merge sort) 시간 복잡도