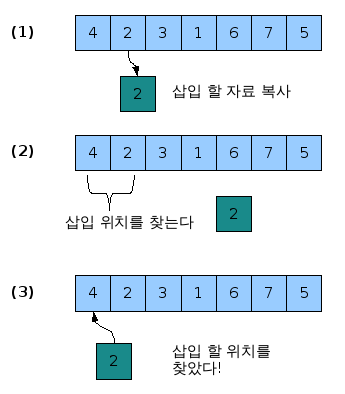
삽입 정렬 (Insertion Sort)
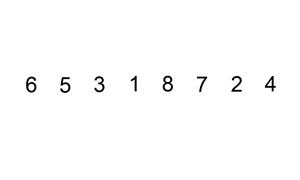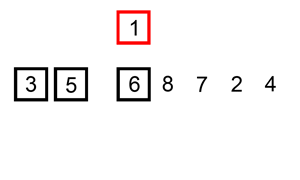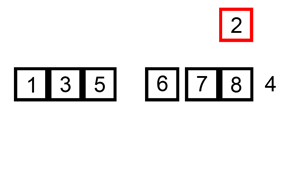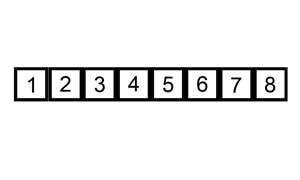
선택 정렬과 함께 인간에게 뭔가를 정렬하라고 하면 무의식으로 사용하는 대표적인 알고리즘이다.
k번째 원소를 1부터 k-1까지와 비교해 적절한 위치에 끼워넣고 그 뒤의 자료를 한 칸씩 뒤로 밀어내는 방식으로,
평균적으론 중 빠른 편이나 자료구조에 따라선 뒤로 밀어내는데 걸리는 시간이 크며,
앞의 예시처럼 작은 값이 뒤쪽에 몰려있으면 (내림차순의 경우 큰 값이 뒤쪽에 몰려있으면) 최악이다.
다만 이미 정렬되어 있는 자료구조에 자료를 하나씩 삽입, 제거하는 경우에는 현실적으로 최고의 정렬 알고리즘이 되는데, 탐색을 제외한 오버헤드가 매우 적기 때문이다.
그밖에도 배열이 작을 경우에 역시 상당히 효율적이다.
일반적으로 빠르다고 알려진 알고리즘들도 배열이 작을 경우에는 대부분 삽입 정렬에 밀린다.
따라서 고성능 알고리즘들 중에서는 배열의 사이즈가 클때는알고리즘을 쓰다가 정렬해야 할 부분이 작을때 는 삽입 정렬로 전환하는 것들도 있다.
또 굳이 장점을 뽑자면 코드 구현이 매우 쉽다.
그 예로 C/C++에서 기본적인 삽입 정렬을 구현하는데는 3~4줄의 코드면 충분하다.
짧은 C++ 삽입 정렬 코드
#include <vector>
template <typename T>
void insertionSort(std::vector<T>& vec, const int& left, const int& right){
for (int i = left; i < right; ++i){
for (int j = i + 1; j > left && vec[j] < vec[j - 1]; --j){
std::swap(vec[j], vec[j - 1]);
}
}
}(구현만 한 코드다.)
https://youtu.be/ROalU379l3U
예제(출처:https://tinyurl.com/yxjnzeqy)

1 싸이클
두 번째 원소인 5를 Key로 해서 그 이전의 원소들과 비교한다.
Key 값 5와 첫 번째 원소인 8을 비교한다.
8이 5보다 크므로 8을 5자리에 넣고 Key 값 5를 8의 자리인 첫 번째에 기억시킨다.
2 싸이클
세 번째 원소인 6을 Key 값으로 해서 그 이전의 원소들과 비교한다.
Key 값 6과 두 번째 원소인 8을 비교한다.
8이 Key 값보다 크므로 8을 6이 있던 세 번째 자리에 기억시킨다.
Key 값 6과 첫 번째 원소인 5를 비교한다.
5가 Key 값보다 작으므로 Key 값 6을 두 번째 자리에 기억시킨다.
3 싸이클
네 번째 원소인 2를 Key 값으로 해서 그 이전의 원소들과 비교한다.
Key 값 2와 세 번째 원소인 8을 비교한다.
8이 Key 값보다 크므로 8을 2가 있던 네 번째 자리에 기억시킨다.
Key 값 2와 두 번째 원소인 6을 비교한다.
6이 Key 값보다 크므로 6을 세 번째 자리에 기억시킨다.
Key 값 2와 첫 번째 원소인 5를 비교한다.
5가 Key 값보다 크므로 5를 두 번째 자리에 넣고 그 자리에 Key 값 2를 기억시킨다.
4 싸이클
다섯 번째 원소인 4를 Key 값으로 해서 그 이전의 원소들과 비교한다.
Key 값 4와 네 번째 원소인 8을 비교한다.
8이 Key 값보다 크므로 8을 다섯 번째 자리에 기억시킨다.
Key 값 4와 세 번째 원소인 6을 비교한다.
6이 Key 값보다 크므로 6을 네 번째 자리에 기억시킨다.
Key 값 4와 두 번째 원소인 5를 비교한다.
5가 Key 값보다 크므로 5를 세 번째 자리에 기억시킨다.
Key 값 4와 첫 번째 원소인 2를 비교한다.
2가 Key 값보다 작으므로 4를 두 번째 자리에 기억시킨다.
코드 구현
# include <stdio.h>
# define MAX_SIZE 5
// 삽입 정렬
void insertion_sort(int list[], int n){
int i, j, key;
// 인텍스 0은 이미 정렬된 것으로 볼 수 있다.
for(i=1; i<n; i++){
key = list[i]; // 현재 삽입될 숫자인 i번째 정수를 key 변수로 복사
// 현재 정렬된 배열은 i-1까지이므로 i-1번째부터 역순으로 조사한다.
// j 값은 음수가 아니어야 되고
// key 값보다 정렬된 배열에 있는 값이 크면 j번째를 j+1번째로 이동
for(j=i-1; j>=0 && list[j]>key; j--){
list[j+1] = list[j]; // 레코드의 오른쪽으로 이동
}
list[j+1] = key;
}
}
void main(){
int i;
int n = MAX_SIZE;
int list[n] = {8, 5, 6, 2, 4};
// 삽입 정렬 수행
insertion_sort(list, n);
// 정렬 결과 출력
for(i=0; i<n; i++){
printf("%d\n", list[i]);
}
}
//https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html파이썬으로도 구현해보자.
numList = [8,9,6,2,5,11,1,3,4,7]
def insertion_sort(A):
for i in range(1, len(A)):
curNum = A[i]
k = 0
for j in range(i-1, -2, -1):
k = j
if A[j] > curNum:
A[j+1] = A[j]
else:
A[j+1] = curNum
break
A[k+1] = curNum
print(numList)
numList = [8,9,6,2,5,11,1,3,4,7]
insertion_sort(numList)
print(numList)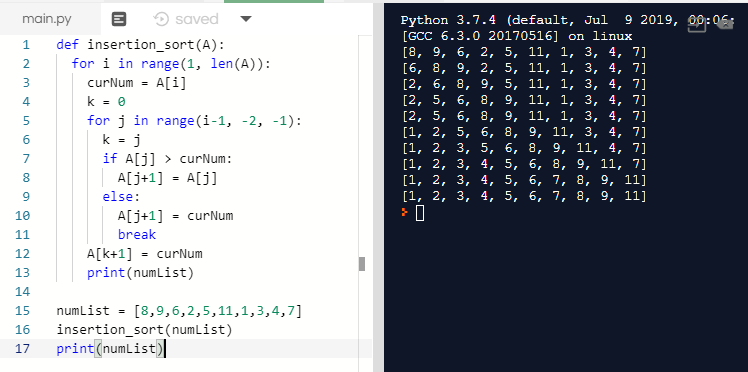
과정 Print, 결과 Print 된 모습이다.
지금 까지 정리
버블정렬,
2019/09/22 - [알고리즘 공부] - 4. 버블 정렬
4. 버블 정렬
버블 정렬(bubble sort) 알고리즘 서로 인접한 두 원소를 검사하여 정렬하는 알고리즘 인접한 2개의 원소를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환한다. 선택 정렬과 기본 개념이 비슷하다. 버블..
blog.tomclansys.com
칵테일정렬,
2019/09/22 - [알고리즘 공부] - 5. 칵테일 정렬
5. 칵테일 정렬
칵테일 정렬(cocktail sort) 셰이커 정렬(shaker sort)라고도 한다. 리플 정렬, 셔플 정렬이라고도 한다. 홀수 번째 돌 때는 앞부터, 짝수 번째는 뒤부터 훑는 정렬. 당연하겠지만 이 정렬은 마지막과 처음이..
blog.tomclansys.com
선택정렬,
2019/09/22 - [알고리즘 공부] - 6. 선택 정렬
6. 선택 정렬
선택 정렬 (Selection sort) 버블 정렬이 비교하고 바로 바꿔 넣는 걸 반복한다면 이 정렬은 1번째부터 끝까지 훑어서 가장 작은 게 1번째, 2번째부터 끝까지 훑어서 가장 작은 게 2번째……해서 (n..
blog.tomclansys.com
삽입 정렬은
(현재 글)
삽입정렬의 경우
최선의 경우에는
비교 횟수: 이동 없이 1번의 비교만 이루어진다.
외부 루프: (n-1)번
즉 시간 복잡도가 O(n)이 된다.
최악의 경우에는. (입력 자료가 역순일 경우)
비교 횟수: 외부 루프 안의 각 반복마다 i번의 비교 수행
외부 루프: (n-1) + (n-2) + … + 2 + 1 = n(n-1)/2 = O(n^2)
교환 횟수: 외부 루프의 각 단계마다 (i+2)번의 이동 발생
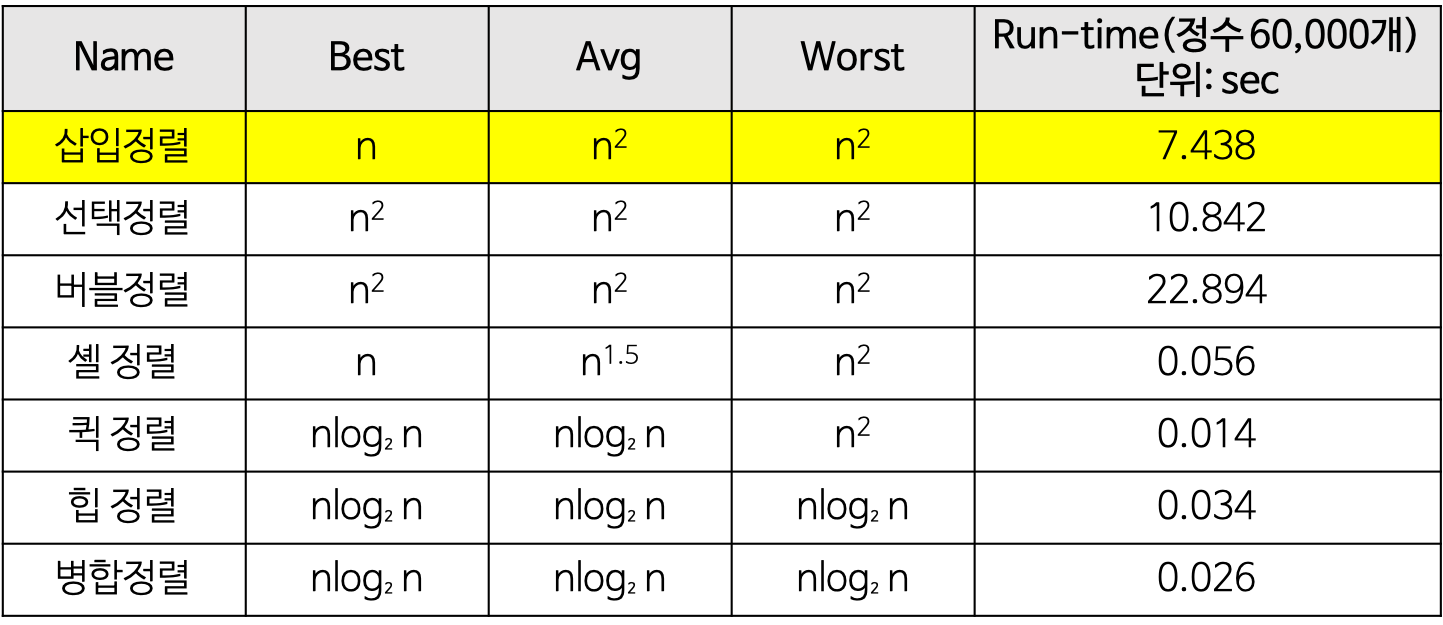
다음은 O(NlogN) 의 시간 복잡도를 가진 것들에 대해 쓸 것이다.
추가)
insertion sort 파이썬 간단 구현
# insertion sort
a = [10, 5, 3, 7, 12, 1, 2, 4, 8]
for i in range(1, len(a)):
for j in range(i):
if a[i]<a[j]:
a.insert(j, a.pop(i))
print(a)결과
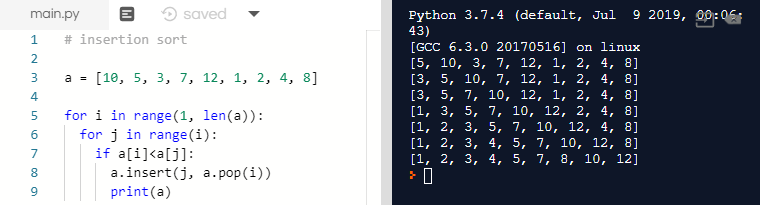
insertion sort with 재귀 함수 파이썬 간단 구현
# insertion sort with Recurrence
def insertionkim(i = 0, j = 0):
global a
print(a)
if j == len(a):
return
else:
if i == j :
insertionkim(0, j+1)
else:
if a[i] > a[j]:
a.insert(i, a.pop(j))
insertionkim(i+1, j)
a = [81, 95, 5621, 1231, 151, 1, 4, 2, 3]
insertionkim()결과




