3. 계산 복잡도 (시간복잡도,공간복잡도) 정리

출처: https://joshuajangblog.files.wordpress.com/2016/09/1.jpg?w=638

---

계산 복잡도 (Computational Complexity)

계산 복잡성, 계산 효율성, 알고리즘 효율성, Time Complexity, 시간 복잡도, 빅 오 표기법

 

컴퓨터 과학에서 계산 이론의 분야로, 계산 문제를 푸는 알고리즘을 복잡도에 따라 문제의 모임을 구성하는 방법을 연구한다.

이 때 알고리즘의 수행은 실제 컴퓨터가 할 수 있지만, 평가하는 데에는 튜링 기계와 관련이 있는 정량화된 방법을 사용한다.

복잡도의 기준은 알고리듬이 소모하는 소요 시간과 메모리 사용량 등의 자원이다.

전자를 시간 복잡도, 후자를 공간 복잡도라 한다.

일반적으로 이와 같은 시공간 등의 자원은 입력의 크기에 의존하는 것으로 취급한다.

https://ko.wikipedia.org/wiki/계산_복잡도_이론

계산 복잡도 이론 - 위키백과, 우리 모두의 백과사전

---

시간 복잡도(時間複雜度)

알고리즘의 소요 시간을 정확히 평가할 수는 없으므로, 자료의 수 n이 증가할 때 시간이 증가하는 대략적인 패턴을 시간 복잡도라는 이름으로 나타내게 된다.

이를 Big-O 표기법(Big O notation)으로 주로 나타낸다.

예를 들어 입력 자료의 크기 n에 대하여 O(n)의 시간복잡도를 가진 알고리즘은 대략 크기 n에 비례하는 수의 연산을 수행한다고 보면 된다.

n 이 값이 커지면 커질수록, 시간복잡도가 복잡한 알고리즘은 수행시간이 급격하게 길어지게 된다.

O(1) < O(log n) < O(n) < O(N log n) < O(n^2) < O(n^3) < O(2^n) < O(n!) 

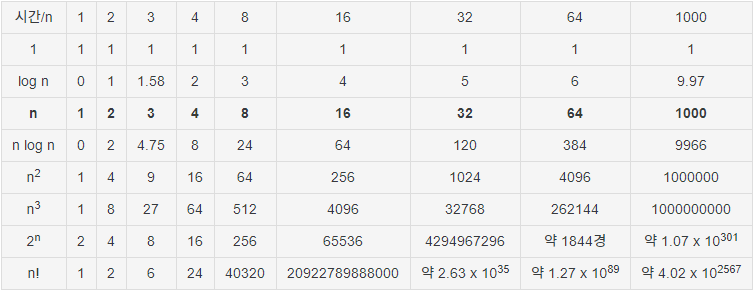
알고리즘의 종류에 따라 시간복잡도의 평가기준도 다양하다.

일반적으로는 O(n)의 시간복잡도를 가지면 좋은 알고리즘으로 취급하며,

log(n)의 지수승이 붙는 정도로 막으면(O(n log n) 등) 매우 좋은 결과이다.

O(n3) 정도만 돼도 큰 자료수에선 급격히 느려진다.

검색 알고리즘의 경우 O(1)이나 O(nlog(n))의 시간복잡도를 가지는 알고리즘을 선호한다.

여기에 해당되는 자료구조/알고리즘에는 해시 테이블과 퀵 정렬 등이 있다.

시간 복잡도가 n의 다항식 이하가 되는 알고리즘들을 다항 시간 알고리즘(polynomial time algorithm)이라고 한다.

여기까지만 보면 다항식과는 다른 증가속도를 자랑하는 O(2n) 또는 O(n!) 같은 알고리즘은 매우 어려워 보이지만,

이런 알고리즘을 쓸 수 밖에 없는 문제들이 수두룩하다.

이런 경우에는 정답을 찾기보단, 근사값을 구해주는 알고리즘을 찾게 된다.

---

공간 복잡도(space complexity)

알고리즘의 공간복잡도는 다음과 같이 정의할 수 있다. 알고리즘이 수행되는데 필요한 메모리의 총량

 

프로그램이 실행될 때 보통 세가지 이유로 컴퓨터 메모리를 사용한다.

1. Instruction Space: 컴파일된 명령어들을 저장하는 메모리의 양
2. Environmental Stack: 함수 호출시 부분적으로 실행 된 함수의 정보를 저장하는 데 사용되는 메모리의 양
3. Data Space: 모든 변수와 상수를 저장하는 메모리의 양

현실에서는 시간 복잡도보다 중요도는 떨어지는데, 시간이 적으면서 메모리까지 지수적으로 증가하는 경우는 없기 때문이고, 다항 시간 내에서 나타나는 메모리 문제들은 보통 알고리즘 자체보다는 알고리즘의 구현에서 발생하는 문제이기 때문이다.

다만 동적 계획법의 경우에는 메모리를 상당히 많이 필요하기 때문에 (공간복잡도가 크기 때문에) 입력 값의 범위가 넓으면 사용하지 못하는 경우가 많다.

또한 임베디드, 펌웨어 등 하드웨어 환경이 매우 한정되어 있을 경우 공간복잡도도 상당히 중요하게 보게된다.

이론적으로는 n에 대한 다항식 만큼의 공간으로도 해결이 안되는 정말 어려운 문제들이 연상된다.

---

정리하면,

- 시간 복잡도(Time Complexity) : 알고리즘의 수행시간 분석결과

- 공간 복잡도(Space Complexity) : 알고리즘의 메모리 사용량에 대한 분석결과

 

알고리즘 트레이닝 사이트에서의 조건.

알고리즘 성능평가는 시간 복잡도와 공간 복잡도를 계산하고 점근적 표기법으로 나타낸다.

점근적 표기법(Asymptotic notations)

오메가 표기

쎄타 표기

---

개인적으로 계산복잡도와 공간 복잡도는 같은것이라고 생각하는데, 엄밀히 따지면 계산복잡도 안에 시간복잡도와 공간 복잡도가 있으므로 계산 복잡도가 더 상위 개념이라고 봐야 한다.

좀 많이 어렵지만, 이론은 항상 이해하기 쉽진 않다. 여러번 보다보면 이해가 될 듯 하다.